Fler bråk ger bättre resultat – i matematiken
Undervisningens innehåll på förskolan och på grundskolans olika stadier tenderar att vara för lika. Detta kan vara en orsak till att eleverna inte utvecklar sin förståelse för matematik från år till år. Så kan man sammanfatta resultatet av ny forskning som Caroline Nagy, universitetsadjunkt vid Högskolan i Halmstad, står bakom. Forskarens rekommendation: Fler bråk i matematikundervisningen – och mindre fokus på pizzabitar och äppelhalvor.
"Kraven får inte vara för höga så att eleverna inte hänger med, och inte för låga så att det inte blir någon utmaning. Kraven ska öka successivt genom skolgången."
– Caroline Nagy
– Det började med att jag råkade öppna en lärobok i matte för elever i årskurs 4 och en lärobok för gymnasieelever. Båda böckerna började på samma nivå! säger Caroline Nagy som nyligen lade fram sin licentiatuppsats.
Progression handlar om att elever successivt möter ökade krav i undervisningen.
– Kraven får inte vara för höga så att eleverna inte hänger med, och inte för låga så att det inte blir någon utmaning. Kraven ska öka successivt genom skolgången.
I sin studie ”Fler bråk i matematikundervisningen – en aktionsforskningsstudie där lärare lär om progression”, har Caroline Nagy undersökt hur bråk lärs ut från förskola till årskurs nio.
Att förstå vad eleverna inte förstår
– Jag har kommit fram till att progressionen inte är optimal och att eleverna har liknande förståelse om bråk, oavsett stadium. Undervisningen som lärarna hade planerat kom inte alltid åt problematiken som eleverna hade i sin förståelse. Kommer man inte åt vad det är eleverna egentligen inte förstår, är det svårt att planera för progression, säger hon.

I studien ser Caroline Nagy att de bilder som läraren visar för eleverna har stor betydelse för elevernas kunskapsutveckling oavsett ålder. Att prata äpplen och pizzabitar är förvisso konkret och tydligt, men det är skillnad mellan vardagen och den praktiska verkligheten jämfört med kraven på exakthet inom matematiken. Samtidigt betonar läroplanen att undervisningen ska kopplas till verkligheten.
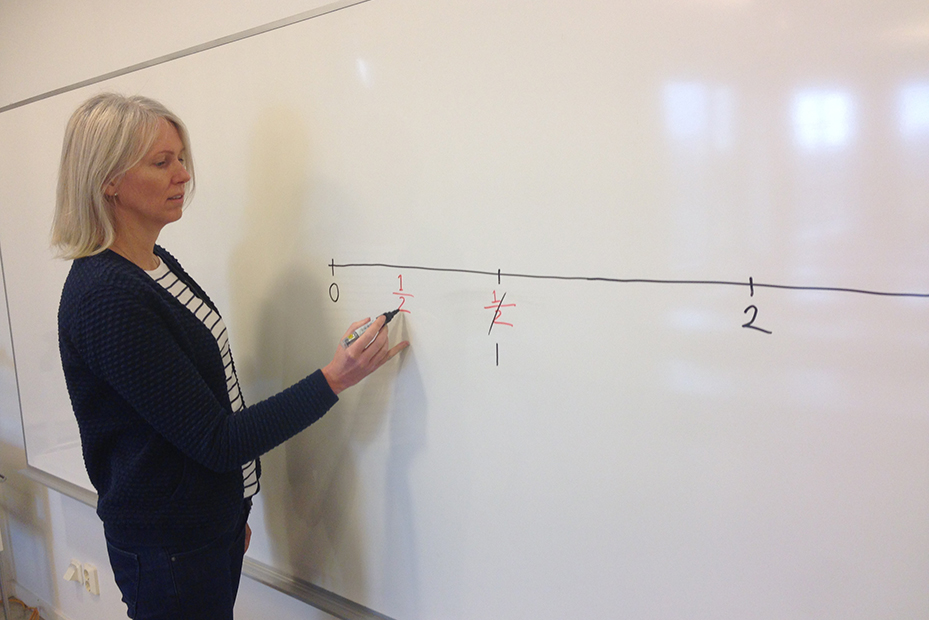
När elever ska placera tal på en tallinje gör de generellt sett samma fel oavsett om de går på lågstadiet eller på högstadiet. Säg att tallinjen går från 0–2. Elever som får i uppgift att markera ½ på tallinjen, har en tendens att välja mitten på tallinjen, som i det här fallet är talet 1. Kanske tänker eleverna att ½ är detsamma som hälften av den visade tallinjen, och då väljer de att markera vid ”en halv tallinje”. Eleverna tänker då inte på att varje punkt har en placering på tallinjen. (Talet ½ är alltid placerad mitt emellan talet 0 och 1).
Tidigare studier visar att elever som får resonera med hjälp av något så konkret som pizzabitar klarar uppgifter i bråk – tas pizzorna bort, är det färre elever som löser uppgifterna korrekt. Caroline Nagys studie visar att pizzorna inte alltid hjälper eleverna att förstå bråk.
– Lärare måste vara noga med vilket material de använder i undervisningen och ha en stor variation i bilder och konkret material. Om vi redan från tidig ålder enbart visar exempelvis en klassisk fjärdedel blir det också svårt med progression. Eleverna får en förståelse som inte är hållbar, säger Caroline Nagy.
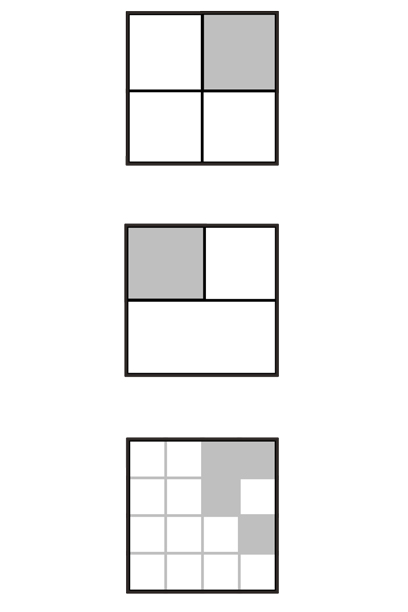
Hur tolkar man vad en bild av vad en fjärdedel är? Det är enkelt med en bild som är delad i fyra lika stora delar. Men hoppar man över en linje, eller placerar ut fyra bitar lite här och var på en bild med 16 delar, blir det genast svårare.
I studien har hon tillsammans med lärare analyserat videofilmad undervisning:
– Det blev nästan en vändpunkt för studien att upptäcka hur lärarna förenklade undervisningen så att den inte längre hjälpte eleverna. Genom att utöka innehållet, göra det mer varierat och också mer komplicerat, blev det en tydligare kunskapsutveckling för eleverna.
Caroline Nagy har hittat få studier som undersöker progression i undervisningen. Det finns inte heller några nationella riktlinjer eller dylikt för innehållet i läroböckerna, utan innehållet bestäms i slutänden av läromedelsförlagen. Byte av lärare kan också påverka progressionen i undervisningen.
Viktigt arbete mellan årskurser
– Ofta byter eleverna lärare i skiftet mellan förskoleklass och lågstadiet, mellan låg- och mellanstadiet och så vidare. Det blir inte alltid så mycket samtal mellan lärarna på olika stadier, och då är det inte lätt för lärarna att bygga på vad som har gjorts tidigare, säger Caroline Nagy.

Caroline Nagy, universitetsadjunkt i utbildningsvetenskap, försvarade sin licentiatuppsats för ett några veckor sedan. I sin studie har hon valt att fokusera på tal i bråkform. Hon menar att fler områden borde studeras utifrån progression i undervisningen. I grunden är Caroline Nagy legitimerad 1–7-lärare och har undervisat på lågstadiet i 15 år. Uppsatsen lades fram vid Högskolan i Halmstad, som också finansierat studien. Forskarutbildningen genomförde dock Caroline Nagy vid Göteborgs universitet.
Att arbeta över årskursgränserna, och gemensamt planera och analysera undervisning är därför en viktig nyckel till progression i undervisningen. En annan viktig faktor handlar om lärares trygghet i ämnet och att identifiera elevernas förståelse. De lärare som inte lyckas urskilja mindre framgångsrika förståelser kan inte heller påverka dessa. Det får därför konsekvenser för elevernas kunskapsutveckling, vilket i sin tur försvårar progression i undervisningen.
Text och bild: KRISTINA RÖRSTRÖM