Skapar ny matematisk teori om samtidiga händelser
Redan som liten ville han fundera ut egna svar, hellre än att fråga någon vuxen. Nu är Johan Thunberg forskare i matematik och arbetar på en ny vetenskaplig teori om synkroniserade system.
Alla jobbar inte precis som jag, så vi kompletterar varandra. Det är bra.
Johan Thunberg, biträdande universitetslektor
– Min fru blir galen på mig ibland när jag sitter och bara försvinner in i mina tankar. Först tyckte hon att det var charmigt, men med tiden började det blir störande. Så det är något jag får jobba på i mitt privatliv …, säger Johan Thunberg.
Johan Thunberg ler lite. Att han helt kan absorberas av en tanke är långtifrån bara ett problem. Det är en tillgång i arbetet som matematiker, och en egenskap som förde honom till det jobb han har i dag. Matematiska frågor har upptagit hans tankar ända sedan gymnasiet och till sist tänkte han att om han ändå inte kunde göra sig av med dem, varför inte syssla med dem på heltid? Nu gör han det, som forskare och lärare vid Akademin för informationsteknologi. Johan Thunbergs största forskningsprojekt just nu handlar om synkronisering och konsensus. ”Nästan global konsensus”, mer exakt.

Johan Thunberg, biträdande universitetslektor vid Akademin för informationsteknologi.
Ett bra ramverk för matematiska modeller
Synkronisering innebär att händelser inträffar samtidigt. Fenomenet finns både i naturen, när till exempel fåglar flyger i flock, och i tekniska och digitala system där det ofta är ett krav att saker sker samtidigt. Synkronisering kan beskrivas med hjälp av matematiska modeller som gör det möjligt att dra slutsatser om systemen.
– Vi kan till exempel ha formulerat en matematisk modell som fungerar givet vissa observationer. Den kanske beskriver enheter som börjar oscillera, alltså svänga, i fas. Kan vi då veta att de kommer att oscillera i fas oavsett startvillkoren, eller råkade de bara göra det i just vår observation? Konvergerar de för nästan alla initialvillkor – eller kan vi bestämma en exakt region där de gör det?
Konvergens betyder i det här sammanhanget att egenskaper hos systemens enheter gradvis blir mer lika. Om de når samma värde kallas det att systemen uppnår konsensus, och om det alltid sker har systemen egenskapen ”global konsensus”.
För att skapa en användbar matematisk modell gäller det att studera ett lagom ramverk. Johan Thunbergs ramverk är något som kallas ortogonala matriser, som kan användas för att beskriva till exempel olika typer av rörelser eller komplexa former. När de används för att beskriva rörelser så konvergerar matriserna ibland till samma värde. För vissa matriser sker det nästan alltid. Bara i teorin kan det finnas undantag. Systemen har alltså egenskapen nästan global konsensus och Johan Thunbergs mål är att utveckla en komplett matematisk teori för detta.
– Global konsensus är väldigt välstuderat redan, men mest för linjära system. Så fort modellen är icke-linjär blir det mycket svårare. Vi vill i vårt forskningsprojekt täcka in nästan alla system av en viss typ och visa vad som är möjligt vad gäller konvergens, säger Johan Thunberg.
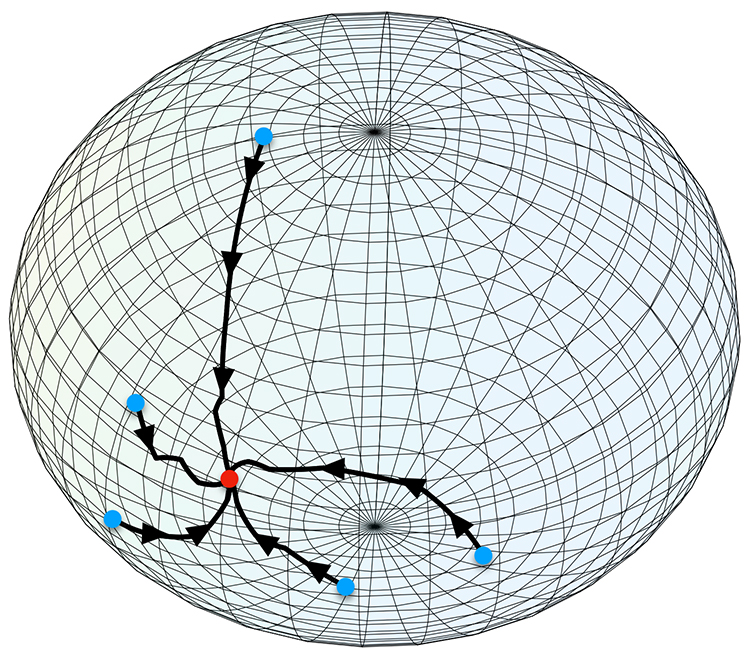
Bilden illustrerar hur fem olika värden konvergerar på en yta av en sfär. De tar olika vägar men slutar ändå i samma punkt.
Man vet aldrig hur teorierna kan tillämpas
När Johan Thunberg tar sig an ett problem brukar han sitta och fundera igenom det innan han börjar skriva ner det. Han beskriver det som att han skapar en mental karta i huvudet över vart han ska, och fixar detaljerna på vägen. Men han har en kollega som i stället räknar sida upp och sida ner för att se var hon hamnar, och andra kollegor som tidigt börjar simulera i matematiska datorprogram för att få bekräftelse på att de är på väg åt rätt håll.
– Alla jobbar inte precis som jag, så vi kompletterar varandra. Det är bra.
Johan Thunberg har funderat på om han kan få in forskningen i sin undervisning, men det är inte helt lätt. Han är lärare för ingenjörsstudenter på första året och de har bara hunnit lära sig grunderna till det som Johan Thunberg arbetar med. Kanske kan han hjälpa dem att få lite fågelperspektiv på det som de gör, se vart de är på väg.
Så fort modellen är icke-linjär blir det mycket svårare.
Målet med forskningen om ortogonala matriser är att göra själva matematiken bättre genom att teorierna blir mer kompletta. Modellerna ska fungerar även för vad som kallas ”högre ordningens rum”, alltså mer än de tre dimensioner vi själva lever i – kanske hundra dimensioner. Då handlar det inte precis om något som kan föras in i ingenjörsvetenskapen, konstaterar Johan Thunberg. Men ibland blir han själv överraskad över hur hans resultat kan användas praktiskt.
– Jag hörde från före detta kollegor att våra tidigare resultat har använts för att lösa ett problem som hade att göra med orienteringen på u-båtar när de roterar under vatten. Så man vet aldrig vad teorierna kan komma att tillämpas på – men någonting blir det, det tror jag!
Text: LISA KIRSEBOM
Bild: MAGNUS KARLSSON och JOHAN THUNBERG
Toppbild: ISTOCK